在法国与西班牙战争期间，他曾破译西班牙作战机密，首次崭露数学才能，但却遭西班牙宗教裁判所缺席判决处以焚烧致死的极刑，幸未能执行。从1584到1589年这段时间，由于政治原因，韦达变成了平民，于是他更加专心于数学研究，有时甚至是几天几夜都不睡觉。他是一位人文主义者，极力主张复古，他还自费印刷、发行自己的著作。

韦达从事数学研究只是出于爱好，然而他却完成了代数和三角学方面的巨著。他的《应用于三角形的数学定律》（1579年）是韦达最早的数学专著之一，是系统论述平面和球面三角学的著作之一。他被称为现代代数符号之父。韦达还专门写了一篇论文“截角术”，初步讨论了正弦，余弦，正切弦的一般公式，首次把代数变换应用到三角学中。他考虑含有倍角的方程，具体给出了将COS（nx）表示成COS（x）的函数并给出当n≤11等于任意正整数的倍角表达式了。

韦达在欧洲被尊称为“代数学之父”，他最重要的贡献是对代数学的推进，他最早系统地引入代数符号，推进了方程论的发展。韦达系统地研究了卡丹、塔泰格利亚、蓬贝利、斯蒂文以及丢番图的著作，并从这些名家、尤其是从丢番图的著作中，获取了使用字母、缩写代数的思想。他主张用“分析”这个术语来概括当时代数的知识内容和方法，而不赞成从阿拉伯承袭而来的algebra这个词。

韦达的《解析方法入门》（1591年）一书是他的最重要的代数著作，也是最早的符号代数专著。该书集中了他以前在代数方面的大成，使代数学真正成为数学中的一个优秀分支。他对方程论的贡献是在《论方程的整理和修正》一书中提出了二次、三次和四次方程的解法。他在书中第一章应用了两种希腊文献：帕波斯的《数学文集》第7篇和丢番图著作中的解题步骤结合起来，认为代数是一种由已知结果求条件的逻辑分析技巧，并自信希腊数学家已经应用了这种分析术，他只不过将这种分析方法重新组织。韦达不满足于丢番图对每一问题都用特殊解法的思想，试图创立一般的符号代数。他引入字母来表示量，用辅音字母B，C，D等表示已知量，用元音字母A（后来用过N）等表示未知量x，而用A quadratus,A cubus   表示 x2、x3 ，并将这种代数称为本“类的运算”以此区别于用来确定数目的“数的运算”。

当韦达提出类的运算与数的运算的区别时，就已规定了代数与算术的分界。这样代数就成为研究一般的类和方程的学问，这种革新被认为是数学史上的重要进步，它为代数学的发展开辟了道路，因此韦达被西方称为"代数学之父"。

1593年，韦达又出版了另一部代数学专著—《分析五篇》（5卷，约1591年完成）；《论方程的识别与订正》是韦达逝世后由他的朋友A.安德森在巴黎出版的，但早在1591年业已完成。其中得到一系列有关方程变换的公式，给出了G.卡尔达诺三次方程和L.费拉里四次方程解法改进后的求解公式。而另一成就是记载了著名的韦达定理，即方程的根与系数的关系式。韦达还探讨了代数方程数值解的问题，1600年以《幂的数值解法》为题出版。 

韦达用“分析”这个词来概括当时代数的内容和方法。他创设了大量的代数符号，用字母代替未知数，系统阐述并改良了三、四次方程的解法，指出了根与系数之间的关系。给出三次方程不可约情形的三角解法。著有《分析方法入门》、《论方程的识别与订正》等多部著作。韦达系统地研究了方程根的多种有理变换，阐述并改进了三、四次方程的解法，指出了根与系数之间的重要关系，即韦达定理。从而使当时的代数学系统化了。

韦达是第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂，也用字母表示一般的系数，他创设了大量的代数符号，带来了代数理论研究的重大进步。《分析方法入门》是韦达最重要的代数著作，也是最早的符号代数专著。他在书的第一章中应用了两种希腊文献，帕波斯的《数学文集》第七篇和丢番图著作中的解题步骤结合起来，认为代数是一种由已知结果求条件的逻辑分析技巧 ，并相信希腊数学家已经应用了这种分析术，他只不过对这种分析方法进行了重新组织。韦达不满足于丢番图对每一问题都用特殊解法的思想，试图创立一般的符号代数。他引入字母来表示量，用辅音字母B，C，D等表示已知量，用元音字母A（后来用过N）等表示未知量x，而用A quadratus,A cubus 表示 x2、x3 ，并将这种代数称为本“类的运算”以此区别于用来确定数目的“数的运算”。

韦达的这套做法后来经过笛卡儿等人的改进，成为现代代数的形式。韦达把他的符号性代数称作“类的筹算术”，以区别所谓具体的所谓“数的筹算术”，从而指出了代数和算术的区别。当韦达提出类的运算与数的运算的区别时，就已规定了代数与算术的分界。这样，代数就成为研究一般的类和方程的学问，这种革新被认为是数学史上的重要进步，它为代数学的发展开辟了道路，因此韦达被西方称为 “代数学之父”。

1593年，韦达又出版了另一部代数学专著--《分析五篇》（5卷，约1591年完成）；《论方程的识别与订正》是韦达逝世后由他的朋友A.安德森在巴黎出版的，但早在1591年业已完成。其中得到一系列有关方程变换的公式，给出了G.卡尔达诺三次方程和L.费拉里四次方程解法改进后的求解公式。而另一成就是记载了著名的韦达定理，即方程的根与系数的关系式。韦达还探讨了代数方程数值解的问题，1591年已有纲要，1600年以《幂的数值解法》为题出版。

韦达在《分析五篇》中曾说明怎样用直尺和圆规作出导致某些二次方程的几何问题的解。同年他的《几何补篇》（Supplementum geometriae）在图尔出版了，其中给尺规作图问题所涉及的一些代数方程知识。

π的研究

韦达对于几何学也有相当多的研究，他最早明确给出有关圆周率π值的无穷运算式，而且创造了一套10进分数表示法，促进了记数法的改革。  

1579年，他给出了圆周率 π 的第一个无穷乘积的表达式，并由此计算得到了精确到16位小数的π值。

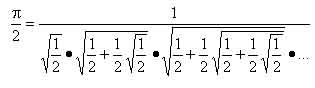
之后，韦达用代数方法解决几何问题的思想由笛卡儿继承，发展成为解析几何学。

最突出的贡献是在符号代数方面。