|
非线性控制理论的发展 人类认识客观世界和改造世界的历史进程，总是由低级到高级，由简单到复杂，由表及里的纵深发展过程。在控制领域方面也是一样，最先研究的控制系统都是线性的。例如，瓦特蒸汽机调节器、液面高度的调节等。这是由于受到人类对自然现象认识的客观水平和解决实际问题的能力的限制，因为对线性系统的物理描述和数学求解是比较容易实现的事情，而且已经形成了一套完善的线性理论和分析研究方法。但是，对于非线性系统来说，除极少数情况外，目前还没一套可行的通用方法，而且每种方法只能针对某一类问题有效，不能普遍适用。所以，可以这么说，我们对非线性控制系统的认识和处理，基本上还是处于初级阶段。另外，从我们对控制系统的精度要求来看，用线性系统理论来处理目前绝大多数工程技术问题，在一定范围内都可以得到满意的结果。因此，一个真实系统的非线性因素常常被我们所忽略了，或者被用各种线性关系所代替了。这就是线性系统理论发展迅速并趋于完善，而非线性系统理论长期得不到重视和发展的主要原因。
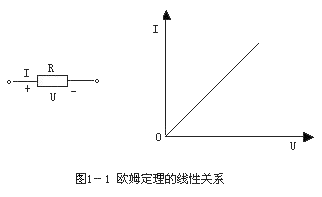
但是，随着科学技术的不断发展，人们对实际生产过程的分析要求日益精密，各种较为精确的分析和科学实验的结果表明，任何一个实际的物理系统都是非线性的。所谓线性只是对非线性的一种简化或近似，或者说是非线性的一种特例。例如一个最简单的大家都熟悉的例子就是欧姆定理。欧姆定理的数学表达式为U=IR。此式说明，电阻两端的电压U是和通过它的电流I成正比，这是一种简单的线性关系，如图1所示。但是，即使对于这样一个最简单的单电阻系统来说，其动态特性，严格说来也是非线性的。因为当电流通过电阻以后就会产生热量，温度就要升高，而阻值随温度的升高就要发生变化。欧姆定理就不再是简单的线性关系了，而是如下式所示的一种非线性关系：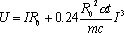
式中，R0是0℃时的电阻数值，mc是电阻的热容量，α为电阻的温度系数，t为电流通过电阻的时间。其非线性关系如图2所示。动力学中的虎克定理、热力学中的第一定律以及气体的内摩擦力等等也都有类似的情况。 对非线性控制系统的研究，到本世纪四十年代，已取得一些明显的进展。主要的分析方法有：相平面法、李亚普诺夫法和描述函数法等。这些方法都已经被广泛用来解决实际的非线性系统问题。但是这些方法都有一定的局限性，都不能成为分析非线性系统的通用方法。例如，用相平面法虽然能够获得系统的全部特征，如稳定性、过渡过程等，但大于三阶的系统无法应用。李亚普诺夫法则仅限于分析系统的绝对稳定性问题，而且要求非线性元件的特性满足一定条件。虽然这些年来，国内外有不少学者一直在这方面进行研究，也研究出一些新的方法，如频率域的波波夫判据，广义圆判据，输入输出稳定性理论等。但总的来说，非线性控制系统理论目前仍处于发展阶段，远非完善，很多问题都还有待研究解决，领域十分宽广。 非线性控制理论作为很有前途的控制理论，将成为二十一世纪的控制理论的主旋律，将为我们人类社会提供更先进的控制系统，使自动化水平有更大的飞越。
|
