|
极点——控制系统的精灵
在实际的应用中,虽然各种控制系统所完成的功能不同,被控制的物理量也未必相同。系统的输出会有许多的变化形式。有的逐渐逼近期望的输出值,有的会在期望值的附近震荡,有的会离期望值越来越远,达不到控制的目的。为什么会有这种不同呢?是什么决定了系统的特性呢?是否有一只神秘的上帝之手在操纵控制系统呢?
 |
|
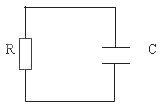
电容放电 |
要回答这个问题,首先得清楚什么叫做微分方程。其实在自然界中,各个物理量之间的变化关系都可以用函数的形式表示,而这些函数同时满足微分方程。让我们看一个简单的例子,图是一个电容C通过电阻R放电的物理过程。根据物理学的知识,电容电压U满足下面的微分方程: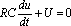 ,我们用数学方法将上面的微分方程解出,就可以求出U按时间变化的过程。微分方程的解的形式是由微分方程的特征方程的解决定的,而特征方程的解就叫做系统的极点。可以按照下面的规则求出一个微分方程的特征方程,把微分符号换成X,几次微分就是X的几次方,保留微分方程的其他部分,就可以得到一个微分方程的特征方程。根据上面的原则,上面例子的特征方程就是:RCX+1=0。解出X的值就是系统的极点。 ,我们用数学方法将上面的微分方程解出,就可以求出U按时间变化的过程。微分方程的解的形式是由微分方程的特征方程的解决定的,而特征方程的解就叫做系统的极点。可以按照下面的规则求出一个微分方程的特征方程,把微分符号换成X,几次微分就是X的几次方,保留微分方程的其他部分,就可以得到一个微分方程的特征方程。根据上面的原则,上面例子的特征方程就是:RCX+1=0。解出X的值就是系统的极点。
系统的极点的形式有实数和复数两种。对于实数的极点,在微分方程的解中就会有一个指数项与它相对应。这个指数是以e为底的,它可以是不断减少的,也可以是不断增大的。对于复数形式的极点,微分方程的解就会有一个振荡的项同它对应,并且振幅会根据复数极点的实部的大小不停的变化。正是由于每个控制系统都有不同的微分方程,从而有不同的极点。这样不同极点对应解的不同部分,这些不同变化特点的部分最终形成了我们能够看到的宏观结果即控制系统的输出。这样使各个控制系统有了千差万别的性能特点。
人们为了使控制系统的性能满足一定的要求,研究了很多控制方法。这些方法虽然采用不同的控制原理,不同的数学方法。但是所有这些方法的最终目的是使系统的极点合理分配,从而得到好的控制效果。所以说极点是决定控制系统性能特点的上帝之手。
[上一页] |
 涓浗绉戝闄㈢鏅簯骞冲彴
涓浗绉戝闄㈢鏅簯骞冲彴
 涓浗绉戝闄㈢鏅簯骞冲彴
涓浗绉戝闄㈢鏅簯骞冲彴